Fidusstrategier til roulette, og hvorfor de ikke virker
- Hvorfor spillere statistisk set taber penge på hvert eneste spil på rouletten
- Roulettestrategier, der ikke virker
- Martingale-strategien på roulette
- Fibonacci-strategien på roulette
- D’Alembert-strategien på roulette
- Labouchere-strategien på roulette
Roulette er et af de mest populære casinospil i verden. Det betyder, at der findes nærmest uendeligt meget materiale om roulette på nettet. En del af materialet er legitimt og præsenterer tingene, som de er i virkeligheden, men der findes desværre også masser af mere eller mindre vildledende websites, der forsøger at narre deres brugere til at tro, at de kan vinde penge på rouletten i det lange løb
Det er nemlig ganske enkelt ikke muligt. Det er umuligt at vinde penge fra casinoet på en korrekt fungerende roulette over tid. Den manglende mulighed for at "slå" rouletten er dybt integreret i spillets matematiske og statistiske fundament. Det kommer vi nærmere ind på senere.
Læs videre, og find ud af, hvorfor det er umuligt at slå rouletten, og hvorfor de oftest markedsførte roulettestrategier ikke virker, selvom de lover kontinuerlige overskud. Når du har læst artiklen til ende, skulle du gerne have overblik over, hvilke strategier du skal undgå og hvorfor, så du ikke lader dig narre af de særdeles fristende, men som oftest vildledende informationer, du kan finde online.
Vi betragter strategierne her i artiklen som uærlige, fordi de ofte lover spillerne store og kontinuerlige gevinster, selvom det er et løfte, de simpelthen ikke kan holde. Der findes imidlertid andre strategier, der kan hjælpe dig med at effektivisere dit spil på rouletten, så du maksimerer dine chancer for at forlade casinoet med en gevinst. Dem har vi samlet i vores artikel om roulettestrategier, der virker.
Hvorfor spillere statistisk set taber penge på hvert eneste spil på rouletten
Vi lægger ud med en forklaring på, hvorfor samtlige spil der placeres på rouletten, giver spilleren et tab på den lange bane. Som tidligere nævnt hænger det sammen med roulettens odds, og hvordan spillet er skruet sammen matematisk.
TBP og husets fordel i roulette
Samtlige spil på et casino kan karakteriseres efter deres såkaldte tilbagebetalingsprocent (TBP), der beskriver, hvor stor en procentdel af spillerens indsats han eller hun statistisk set vinder tilbage. Hvis et spil har en TBP på 100 %, er chancen for at vinde og tabe den samme. Casinospil har imidlertid altid (med et par særdeles sjældne undtagelser) en lavere TBP.
Roulette er ikke en af undtagelserne. TBP i europæisk roulette er 97,3 %, mens TBP i amerikansk roulette er helt nede på 94.74 %. Det betyder, at hver gang du spiller for 100 kr., "vinder" du statistisk set 97,30 kr. i europæisk roulette eller 94,74 kr. i amerikansk roulette. Da gevinsten er mindre end indsatsen, er det ikke svært at se, at du statistisk set taber penge på hvert eneste spil på rouletten.
Husets fordel er den statistiske fordel, casinoet har i forhold til spillerne. Den kan beregnes som:
Husets fordel = 100 % - TBP
Det betyder, at huset har en fordel på 2,7 % i europæisk roulette og en fordel på 5,26 % i amerikansk roulette. Med andre ord vinder casinoet i det lange løb 2,70 kr., hver gang du spiller for 100 kr. på europæisk roulette, og 5,26 kr., hver gang du spiller for 100 kr. i amerikansk roulette.
Du kan læse mere om både TBP og husets fordel i vores artikel om odds på rouletten.
I forhold til resten af denne artikel er det dog nok, at du ved, at det er umuligt at slå rouletten over tid, fordi du statistisk set taber penge på samtlige dine spil, uanset hvor meget du satser, og hvilken type spil du vælger. Det er simpelthen ikke til at komme udenom.
Roulettestrategier, der ikke virker
Nu kommer vi så endelig til de specifikke roulettestrategier, der i virkeligheden ikke virker, selvom de ofte præsenteres som den sikre vej til guld og grønne skove på casinoet.
Du kan læse om følgende for hver af de fire fidusstrategier til rouletten:
- Hvordan strategien angiveligt fungerer, og hvordan den bruges
- Hvorfor strategien alligevel ikke virker og ender med at koste dig penge
- Simulationer af strategien, der tydeligt illustrerer, hvorfor du altid kommer til at tabe dine penge på den lange bane
Hvorfor er de pågældende strategier så populære?
Mange websites præsenterer strategierne som en sikker metode til at vinde penge på internettet, fordi deres eneste mål er at få dig til at oprette en konto på et casino via deres link, så de selv kan tjene penge. De er ligeglade med, at de lyver for deres læsere, og fidusstrategierne her i artiklen kan virke særdeles fristende ved første øjekast – især når de ledsages af mere eller mindre vildledende oplysninger.
Det er derfor, fidusstrategierne forherliges af så mange websites, og derfor du bør tage alle oplysninger om de pågældende strategier med et stort gran salt, når du læser om dem andre steder.
Martingale-strategien på roulette
Den mest populære af alle de mange fidusstrategier til rouletten er uden tvivl Martingale (eller dobbelt op-strategien til roulette, som den også kaldes). Årsagen til strategiens store popularitet er nok, at den både er simpel og kan bruges af stort set alle uden research og forberedelse.
Martingale-strategien fungerer på følgende måde:
- Du placerer din første indsats – eksempelvis 10 kr. – på et af roulettens spil med lige chance (rød/sort, lige/ulige, høj/lav). Farvespillet på enten rød eller sort er det mest brugte, men statistisk set er det ligegyldigt, hvilket af de tre spil du vælger.
- Hvis du vinder, går du tilbage til udgangspunktet og satser 10 kr. igen. Hvis du taber, fordobler du din indsats, og sådan fortsætter du, indtil du vinder. Efterfølgende går du tilbage til udgangspunktet og satser 10 kr. igen.
Martingale-strategien fungerer i cyklusser. Længden af den enkelte cyklus varierer, men de ender altid ud i, at du enten vinder 10 kr., eller taber alt, hvad du har. Vi lægger ud med at se på, hvad der sker, når du vinder.
Her er en række eksempler på cyklusser af Martingale, der ender med overskud:
- Du satser 10 kr. og vinder 20 kr. Din nettogevinst er 10 kr.
- Du satser 10 kr. og taber. Du satser 20 kr og vinder 40 kr. Du har altså satset 30 kr. i alt og vundet 40 kr. Din nettogevinst er 10 kr.
- Du satser 10 kr. og taber. Efterfølgende satser du 20 kr., 40 kr., 80 kr., 160 kr., 320 kr., 640 kr., 1280 kr., 2560 kr. og taber dem allesammen. Til sidst satser du 5120 kr. og vinder 10240 kr. Du har altså satset 10230 kr. i alt og vundet 10240 kr. Din nettogevinst er 10 kr.
Du lykkedes dig altså at få overskud i alle tre eksempler, men det er nok ikke svært at forestille sig, at det sidste eksempel var en noget mere nervepirrende omgang end de to første. Du tabte ni spil i træk, inden lykken vendte, og du vandt det tiende. Du var altså ude i at satse 5120 kr. for at vinde en rund tikrone i den aktuelle cyklus. De hastigt stigende indsatser er et de største problemer ved Martingale-strategien.
Hvorfor Martingale-strategien ser ud til at fungere
Der er en fin logisk forklaring på, hvorfor Martingale burde virke. Hvis du bliver ved med at fordoble din første indsats, må roulettekuglen før eller siden lande på et nummer, der giver dig gevinst. Ikke?
Det er fuldstændig korrekt. Efterhånden som antallet af spil nærmer sig det uendelige, nærmer risikoen for fiasko sig mere og mere 0. Det betyder, at du med uendelige midler og ingen begrænsninger fra casinoet i sidste ende altid vil være i stand til at afslutte en cyklus med en nettogevinst på 10 kr.
Med andre ord fungerer systemet altså, så længe du har adgang til ubegrænsede pengesummer, og casinoet lader dig spille, som du vil. Sådan foregår det bare ikke i den virkelige verden. Du kommer til at løbe ind i problemer, og dem kigger vi nærmere på nu.
Problem #1: Begrænsede midler
I den virkelige verden er der en grænse for, hvor mange penge du har til rådighed. Hvis du spiller efter Martingale-strategien, vil du på et tidspunkt løbe tør for penge, så du ikke længere har råd til at placere den næste indsats i vindercyklussen.
Vi tager et eksempel. Du har 10.000 kr. og spiller efter Martingale-strategien med en første indsats på 10 kr. Med 10.000 kr. på lommen har du råd til at placere følgende indsatser efter hinanden: 10 kr., 20 kr., 40 kr., 80 kr., 160 kr., 320 kr., 640 kr., 1280 kr. og 2560 kr. Det giver en samlet indsats på 5110 kr., men når du har tabt dem, har du kun 4890 kr. tilbage, og du kan derfor ikke placere den næste indsats, der skulle have været 5120 kr.
I vores beregninger her i artiklen vælger vi dog at se bort fra den mulighed og betragter ovenstående situation som et tab. Modsat har vi i simulationerne nedenfor givet de simulerede spillere mulighed for at fortsætte med at spille ved at satse deres resterende penge, selvom de ikke har råd til en fuld indsats efter Martingale-strategien.
Nu kan du selvfølgelig sige, at der ikke er en ret stor risiko for, at du løber ind i en sekvens som ovenstående. Du skal trods alt tabe ni gange i træk. Ved første øjekast kunne det da også se ud, som om det aldrig kunne ske, men det gør det nu altså alligevel. Og det sker endda oftere, end man skulle tro.
Risikoen for at tabe et spil med lige chance 9 gange i træk på europæisk roulette er:
(19/37)^9 = 0,0025 = 0,25 %
Ja, det er et lille tal, men det betyder alligevel, at 1 ud af rundt regnet 402 Martingale-cyklusser statistisk set vil resultere i 9 tabte spil i træk, så du ikke længere har råd til den næste indsats.
Hvis vi justerer lidt på tallene og giver dig 10230 kr. som udgangspunkt i stedet for de runde 10000 kr., så du har råd til at placere et 10. spil på 5120 kr. efter at have tabt de ni forudgående spil, vil det kun være 1 ud af rundt regnet 784 cyklusser, der ender med, at du ikke har råd til den næste indsats.
Risikoen for at tabe en cyklus med mange penge på lommen er altså temmelig lav. Hvis du vil vinde penge i længden med Martingale-strategien, er du imidlertid nødt til at gentage processen tusindvis af gange, og før eller siden går det altså galt. Det illustrerer simulationerne af Martingale-strategien senere i artiklen med al tydelighed.
Problem #2: Indsatsgrænser
Udover udfordringerne med at have penge nok kan du også løbe ind i problemer med casinoets indsatsgrænser, når du spiller efter Martingale-strategien. Minimum- og maksimumindsatsen varierer selvfølgelig fra casino til casino og fra spil til spil, men generelt accepterer de fleste casinoer kun en maksimumindsats, der er et par hundrede gange højere end deres minimumindsats.
Hvis du spiller på online casinoer, kan du til dels undgå problemet ved at spille flere forskellige roulettespil med forskellige indsatsgrænser. Det er ikke særlig praktisk, men det giver dig en mulighed for at reducere indsatsgrænsernes indvirkning på Martingale-strategiens effektivitet.
Selvom du spiller på flere rouletteborde samtidig for at komme udenom indsatsgrænserne, vil din maksimumindsats dog stadig være begrænset. Selv med uendelige midler til rådighed (så du ikke påvirkes af tidligere nævnte problem #1) vil du altså stadig være begrænset af den maksimalt tilladte indsats på det største roulettebord, du kan finde.
Problem #3: Ikke at vide, hvornår du skal stoppe
Som du nok allerede har bemærket, er risikoen for at tabe 9 eller 10 spil i træk ikke særlig stor. Dermed er risikoen heller ikke ret stor for, at det går galt i løbet af 100 cyklusser. Hvis du har penge nok til at placere 10 spil i træk efter at have tabt alle dine tidligere spil (mellem 10230 kr. og 20460 kr.), og du kun går efter at vinde 1000 kr. i alt, vil din sandsynlighed for at vinde faktisk være:
(1-(19/37)^10)^100 = 0,88 = 88 %
Hvis du går efter at vinde 1000 kr., vil din succesrate altså være 88 %. I de resterende 12 % af tilfældene ender du med at tabe så mange penge, at du ikke har råd til at spille videre.
Med et mål på 2000 kr. har du 77,5 % chance for at opnå det, med et mål på 5000 kr. er din chance 52,8 %, og med et mål på 10000 kr. er din chance 27,9 %. Som du kan se, falder sandsynligheden for, at du opnår dit mål logisk nok, i takt med at dit mål stiger.
Problem #3 med Martingale-strategien udløses især af, at den som regel virker i begyndelsen, så spillerne bliver for selvsikre og tror, at den kommer til at virke for evigt. Det er desværre ikke tilfældet. Hvis du spiller efter Martingale-strategien længe nok, kommer du til at tabe alle dine penge.
Hvis du kunne forudse, hvornår du burde forlade casinoet, ville du praktisk taget altid ende ud med overskud. Der er imidlertid ikke noget optimalt tidspunkt at stoppe med at spille på, fordi du aldrig kan vide, hvornår du løber ind i en taberstime. Der er desuden heller ingen garanti for, at du ikke taber alt i den første cyklus af Martingale-strategien.
Simulationer af Martingale-strategien
Vi har simuleret 5 spillere, der spiller efter Martingale-strategien på europæisk roulette ud fra følgende forudsætninger:
- Hver spiller har $1000 til at begynde med og benytter $1 som første indsats.
- Simulationerne stopper efter 10.000 runder på rouletten, eller når spilleren har tabt alle sine penge.
- Spillerne følger Martingale-strategien i forhold til spil og indsatser.
- Hvis spillerne ikke har tilstrækkelige midler til at placere deres næste indsats, satser de alt, hvad de har tilbage. Hvis de taber her, er de ude. Hvis de vinder, fortsætter de efter Martingale-strategien og satser $1 i næste runde.
- Vi har udført simulationerne med vores egen simulationssoftware, der benytter en tilfældighedsgenerator til at afgøre udfaldet af de enkelte runder. Det gælder for øvrigt for alle simulationerne i artiklen. I roulette genereres de tilfældige tal af selve roulettehjulet, men resultaterne er statistisk set de samme.
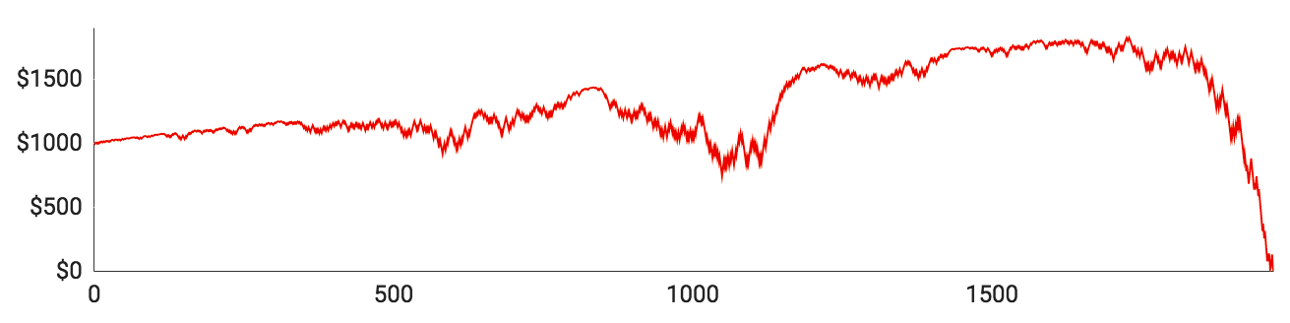
Lad os tage et kig på resultaterne:
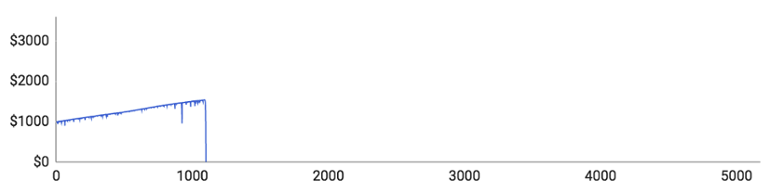
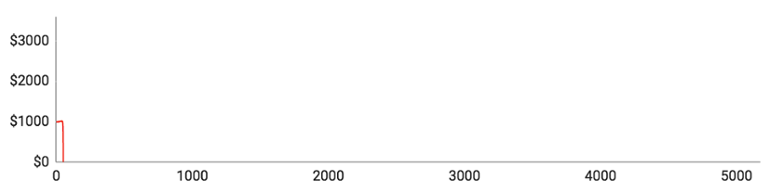
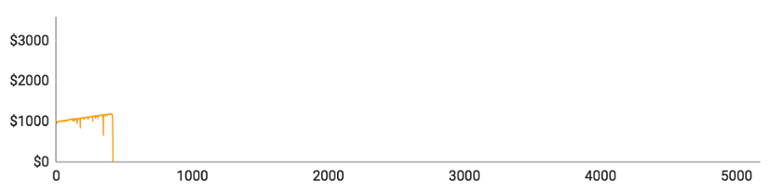
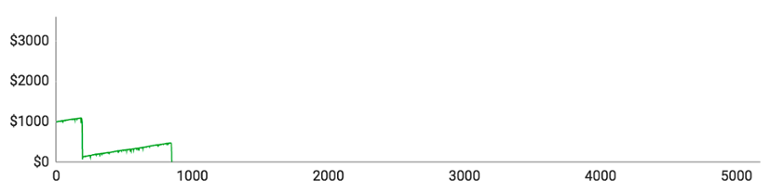
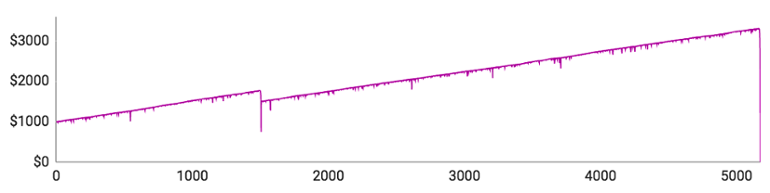
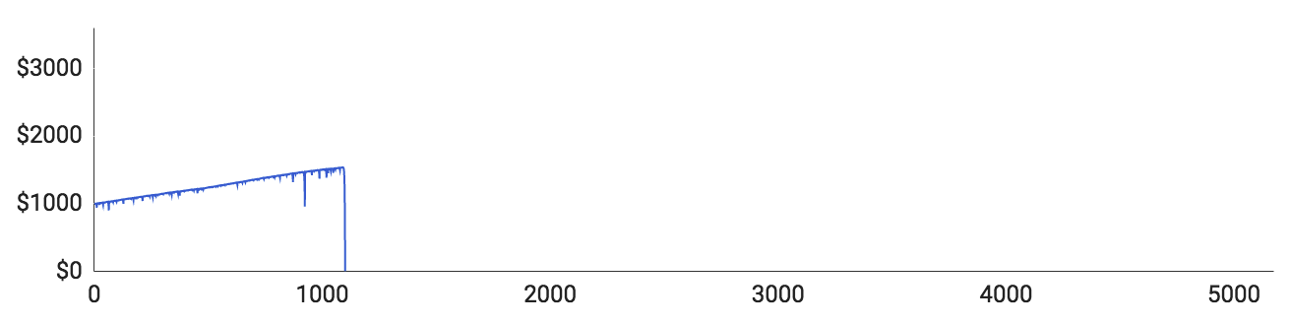
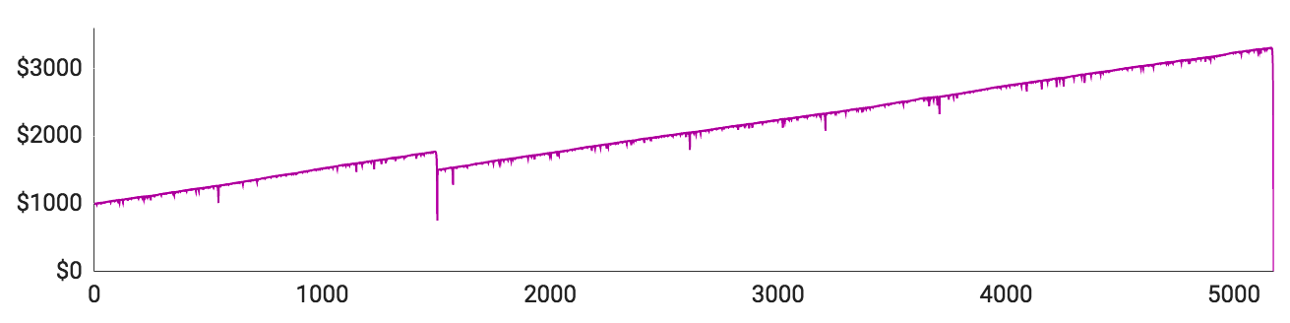
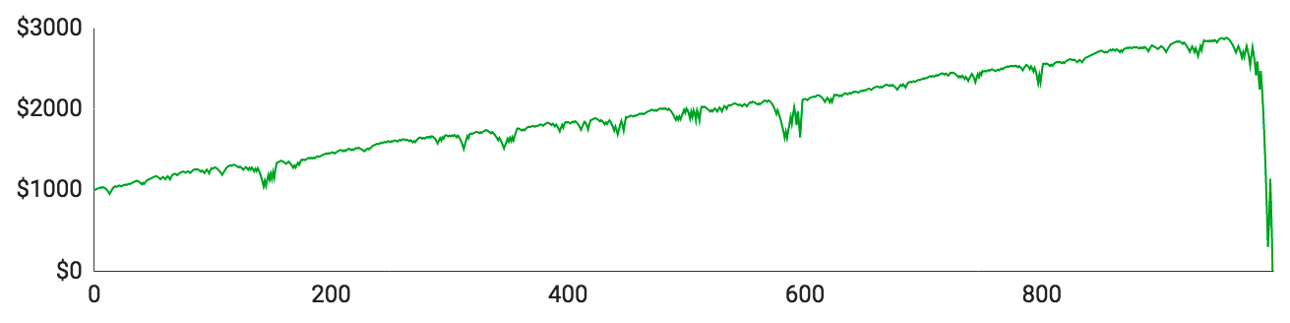
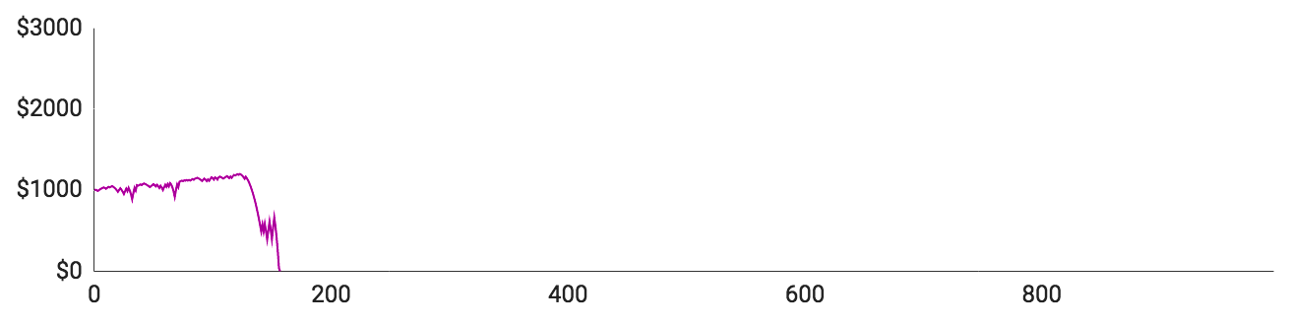
Som du kan se, tabte samtlige spillere alle deres penge, inden de nåede igennem 10.000 runder. Der var dog markante individuelle forskelle undervejs i forløbet:
- Spiller #1 lagde fint ud og nåede op over $1500 med kun en enkelt længere taberstime. Så tabte han imidlertid 11 runder i streg og gik direkte fra $1540 til et stort rundt $0.
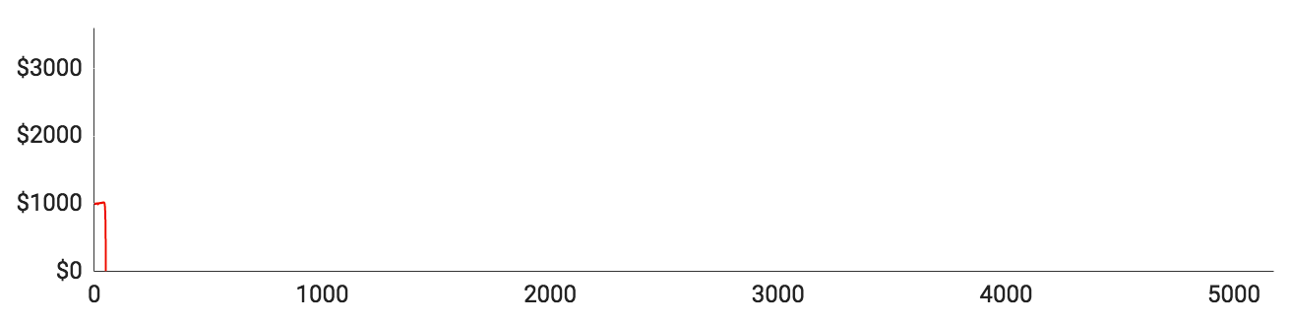
- Spiller #2 gik det endnu værre. Det tog ham kun 51 runder at tabe alle sine penge. Selvom det er en yderst sjælden oplevelse, er det en god påmindelse om, at det kan gå galt lige fra begyndelsen.
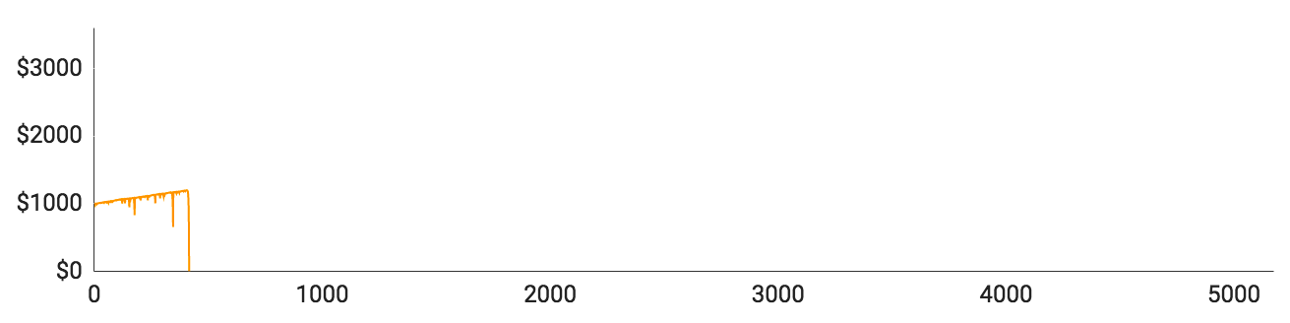
- Spiller #3 formåede at tabe alle sine penge på 417 runder. Han løb ind i en enkelt længerevarende taberstime, som han klarede sig igennem, men blev så ramt af 11 tabte runder i træk kort efter.
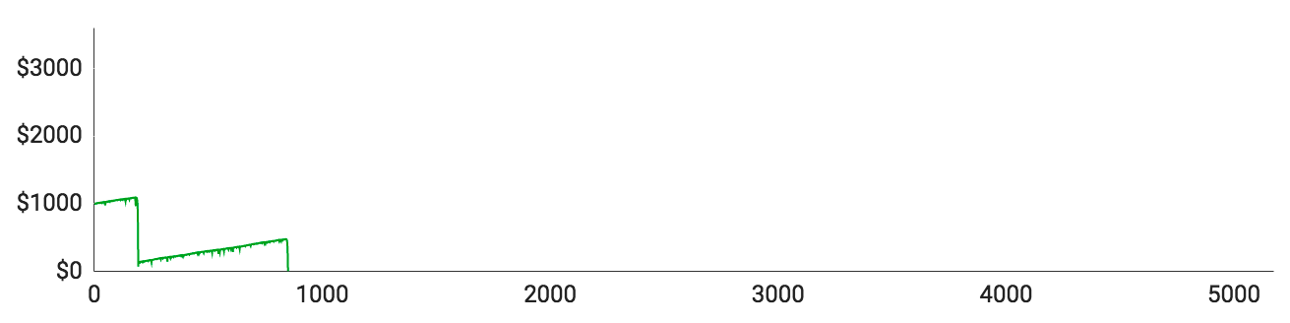
- Spiller #4 gik næsten fallit i hans 193. runde, der efterlod ham med sølle $70 tilbage. Så begyndte han langsomt at bygge sin saldo op igen, men nåede kun til $477, inden en ny taberstime sendte ham ned på $0.
- Spiller #5 klarede sig bedst af alle, men fik alligevel ingen penge med sig hjem. Han nåede op på $3308, inden han blev ruineret af 12 tabte runder i træk.
Ovenstående illustrerer med al tydelighed, at Martingale-strategien ikke rigtig fungerer i det lange løb. Alle spillerne byggede langsomt deres pengebeholdning op, men blev så ramt af en brutal taberstime, der tog alt, hvad de ejede og havde. De lange taberstimer synes nok umiddelbart usandsynlige, men de dukker altså alligevel op ret tit, hvis du spiller længe nok.
Fibonacci-strategien på roulette
Fibonacci-strategien ligner på mange måder Martingale-strategien på rouletten, men der er alligevel visse forskelle, og det er dem, vil vil fokusere på her.
Vi lægger ud med en kort beskrivelse af, hvordan Fibonacci-strategien fungerer. Den er baseret på den berømte talrække, der går under navnet Fibonacci-tal. Talrækken ser således ud:
1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – 89 – 144 – 233 – 377 – 610 – 987 – …
Den kvikke læser har nok allerede bemærket, at de respektive tal i rækken udgør summen af de to foregående tal. Det er den sammenhæng, strategien bygger på, selvom det måske ikke er åbenlyst ved første øjekast.
Fibonacci-strategien fungerer på følgende måde:
- Du lægger ud med at placere en indsats, der svarer til det første tal i talrækken.
- Hvis du taber, går du videre til det næste tal i rækken og spiller for et tilsvarende beløb. Hvis du vinder, går du to tal bagud i talrækken i stedet for. Hvis du når begyndelsen af talrækken, fortsætter du bare med at spille for et beløb, der svarer til det første tal, indtil du taber og kan gå frem efter strategien igen.
Fibonacci-strategien er ikke helt så nem at spille efter som Martingale-strategien. Her er et par eksempler, der kan give dig en idé om, hvordan det foregår.
- Du satser 10 kr. og vinder. Cyklussen er slut, og du begynder forfra på talrækken.
- Du satser 10 kr. og taber. Derefter satser du 10 kr. igen (men denne gang svarer din indsats til det andet tal i rækken, ikke det første – det er vigtigt) og vinder. Du skulle nu gå to tal tilbage i rækken, men da der kun er ét (1), går du tilbage til det og satser 10 kr. igen. Hvis du vinder er cyklussen slut, og du begynder forfra.
- Du satser 10 kr. og taber. Du satser derefter 10 kr., 20 kr., 30 kr., 50 kr., 80 kr., 130 kr., 210 kr. og 340 kr., men taber hver eneste gang. Først ved en indsats på 550 kr. får du endelig gevinst. Herefter går du tilbage til en indsats på 210 kr. og fortsætter efter strategien.
Fordele og ulemper ved Fibonacci-strategien
Der er én markant forskel på at bruge hhv. Martingale og Fibonacci som strategi på rouletten. Hvor der med Martingale bare skal et enkelt gevinstgivende spil til at afslutte en vindercyklus, er en vindercyklus i Fibonacci-strategien først afsluttet, når du når tilbage til begyndelsen af talrækken og vinder et spil, der svarer til det første tal. Med andre ord er en enkelt gevinst ikke nok til at vende en stime af tab.
Alt andet lige kræver det altså flere runder på rouletten at opnå et bestemt overskud med Fibonacci-strategien end med Martingale-strategien. Det betyder dog også, at Fibonacci-strategien er mindre risikabel.
Simulationer af Fibonacci-strategien
Simulationerne af Fibonacci-strategien er udført på stort set samme måde som simulationerne af Martingale-strategien. Den eneste forskel var de 5 simulerede spilleres strategier.
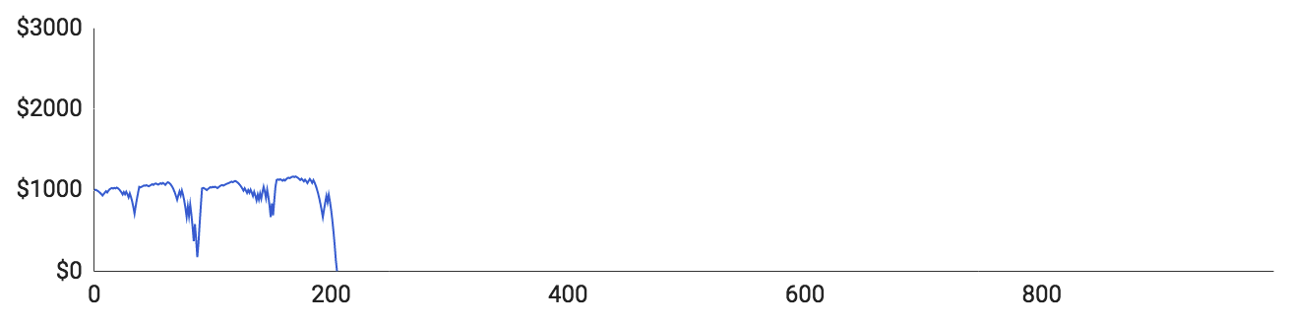
Lad os tage et kig på resultaterne:


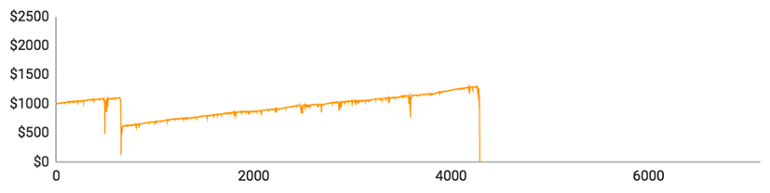

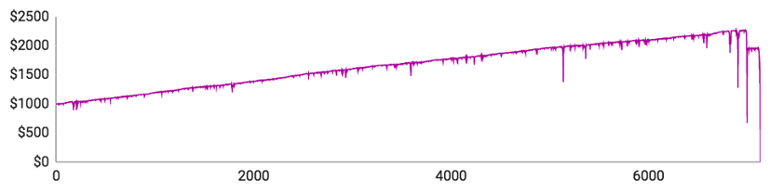
Graferne ligner på mange måder graferne for de spillere, der spillede efter Martingale-strategien, men der er alligevel visse forskelle:
- Graferne stiger lidt langsommere. Det falder fint i tråd med, at Fibonacci-strategien er mindre risikabel og kræver flere runder for at opnå samme overskud.
- Graferne for Fibonacci-strategien er mere forskellige. Med Martingale voksede de forskellige spilleres saldo i nogenlunde samme tempo, indtil de pludselig faldt til nul. Fibonacci-spillerne oplever derimod en mere ujævn stigning, fordi en enkelt gevinst ikke er nok til opveje en serie af tab.
Lad os tage et kig på de fem spillere hver for sig:
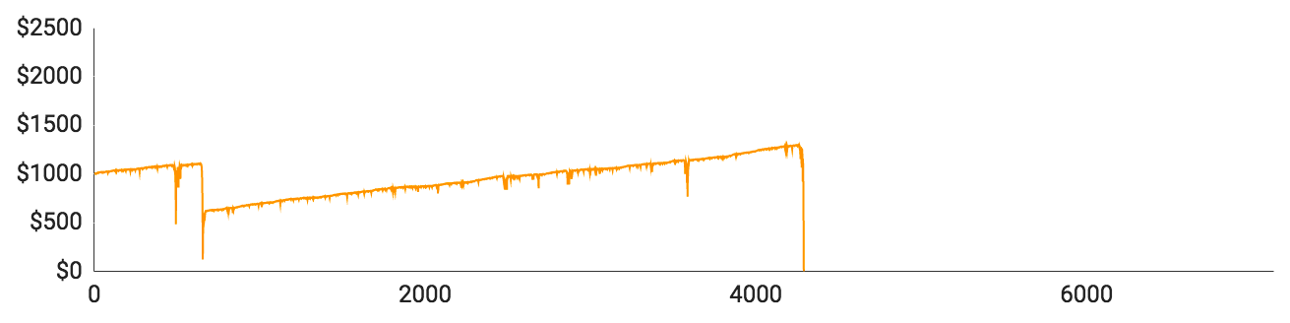
- Spiller #1 var den første, der tabte alle sine penge. Det tog ham bare 488 runder at gå fallit, og han havde på intet tidspunkt nogen form for betydeligt overskud. Det højeste, han nåede op på, var $1074. Til sidst sendte 11 tabte runder i streg ham ned fra $1067 til $0.
- Spiller #2 klarede sig bedre. Han fik spillet 2291 runder, inden han havde tabt det hele, og han var oppe på $1330, 27 runder inden det gik galt. Ud af de sidste 27 runder vandt han kun de 4, og han var derfor nødt til at spille for højere og højere beløb, så han tabte hurtigere og hurtigere.
- Spiller #3 fik spillet 4290 runder, men han nåede aldrig over $1298, hvilket var mindre end spiller #2’s toppunkt. Det skyldes, at han næsten gik fallit tidligt i forløbet og var nødt til at gå all in med bare $122 i hans 656. runde. Den vandt han, men hans langsomme comeback blev altså senere ødelagt af en dårlig stime, der tog alle hans penge.
- Spiller #4 tabte alt på 1272 runder. Da det gik bedst, var han oppe på $1175. Han var nødt til at gå all in med $145 i sin 1176. runde, og selvom han vandt den, gik det hele alligevel tabt inden for de næste 100 runder.
- Spiller #5 klarede sig bedst af alle. Han nåede op på hele 7132 runder og havde hele $2269 på kontoen, da han var på sit højeste. Desværre nåede han ikke helt igennem de 10.000 runder, da også han blev ramt af en uheldig stime, der kostede ham alt, hvad han havde.
I sidste ende ligner Fibonacci-strategien altså på mange måde Martingale-strategien, bortset fra at alt stiger og falder lidt langsommere. Saldoen på din konto stiger langsommere, men dine indsatser stiger også langsommere, når du er inde i en dårlig time. Det er derfor, at de simulerede spillere i gennemsnit nåede at spille et større antal runder uden at opnå helt så store overskud som de spillere, der spillede efter Martingale-strategien.
D’Alembert-strategien på roulette
Både Martingale-strategien og Fibonacci-strategien går ud på at forhøje eller reducere din indsats alt efter resultatet af den foregående runde. D’Alembert-strategien fungerer på samme måde, men med en noget mindre forskel på de satsede beløb. Derfor er D’Alembert-strategien meget mindre risikabel.
D’Alembert-strategien baserer sig også på spil med lige chance (rød/sort, lige/ulige, høj/lav). Den fungerer på følgende måde:
- Du placerer din første indsats på et spil med lige chance.
- Hvis du taber, forhøjer du din indsats med 1 enhed i den følgende runde. Hvis du vinder, reducerer du din indsats med 1 enhed i den følgende runde.
Vi tager udgangspunkt i en første indsats på 60 kr. og sætter forhøjelsen/reduktionen til 10 kr. I første runder satser du 60 kr. og taber. Så satser du 70 kr. og taber. Så satser du 80 kr. og vinder. Så satser du 70 kr. og taber. Så satser du 80 kr. og vinder. Så satser du 70 kr. og vinder. Du har nu foretaget 6 spil i alt, hvoraf du har vundet 3 og tabt 3. Selvom du har vundet og tabt lige meget, har du alligevel opnået et overskud på 30 kr. Det er det, strategien udnytter.
Hvis du spiller efter D’Alembert-strategien på rouletten og vinder lige så mange runder, som du taber, opnår du et samlet overskud, der svarer til det antal runder på rouletten, du har vundet/tabt. Hvis du vinder 10 runder og taber 10 runder, har du altså et overskud på 10 enheder uanset størrelsen på din første indsats.
Det lyder umiddelbart godt, fordi du bare skal vinde lige så tit, som du taber, for at opnå overskud. De såkaldte spil med lige chance giver dig imidlertid ikke en 50:50 chance for at vinde (på trods af deres navn). Statistisk set vinder du nemlig kun 48,65 % af runderne på europæisk roulette, mens du taber de resterende 51,35 %. Selvom forskellen ikke er stor, er det nok til, at D’Alembert-strategien ikke er profitabel i det lange løb.
Fordele og ulemper ved D’Alembert-strategien
Fordelen ved D’Alembert-strategien er, at den er meget mindre risikabel end både Martingale og Fibonacci. Der er selvfølgelig stadig en risiko, men fordi dine indsatser ikke stiger så hurtigt i dine taberstimer, behøver du ikke at have så mange penge på din konto til at begynde med. Du har mindre risiko for at gå fallit, og du kommer sandsynligvis heller ikke til at få problemer med roulettebordets maksimum- og minimumindsatser.
Den langsomme stigning i indsatser kan til gengæld også være en ulempe. Først og fremmest kommer du sandsynligvis ikke til at vinde ret mange penge med strategien – i hvert fald ikke set i forhold til din første indsats og det antal runder, du er nødt til at spille.
Hvis du løber ind i en række tab, får du desuden særdeles svært ved at nå tilbage til et overskud igen. Det kræver faktisk en betragtelig vinderstime. Og det skal ses i forhold til den ene gevinstgivende runde, der er nødvendig for at vende minus til plus i Martingale-strategien. Det kræver lidt mere med Fibonacci, men der er stadig langt op til det antal vundne runder, der er nødvendige i D’Alembert-systemet.
Simulationer af D’Alembert-strategien
Simulationerne af D’Alembert-strategien kunne ikke tage udgangspunkt i en første indsats på $1, fordi indsatsen skulle reduceres, når spillerne vandt. Med en første indsats på $1 var der ikke plads til, at indsatsen kunne blive lavere. Den første indsats kunne dog heller ikke være ret meget højere end $1, hvis resultaterne stadig skulle være sammenlignelige med de øvrige strategier.
Vi valgte derfor en første indsats på $5 og gav spillerne et startbeløb på $1000. Spillerne fulgte D’Alembert-strategien, og hvis de nåede ned til en indsats på $1, blev de bare ved med at satse $1, indtil de tabte en runde og kunne sætte deres indsats op.
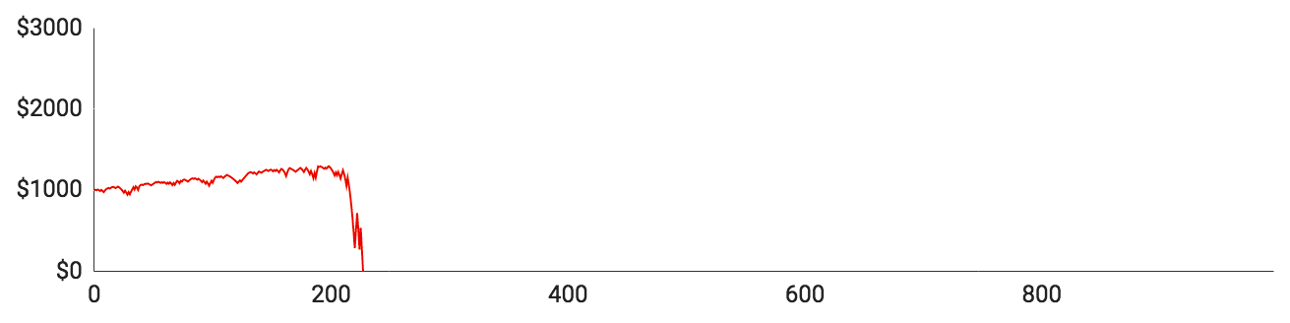
Her er resultaterne:
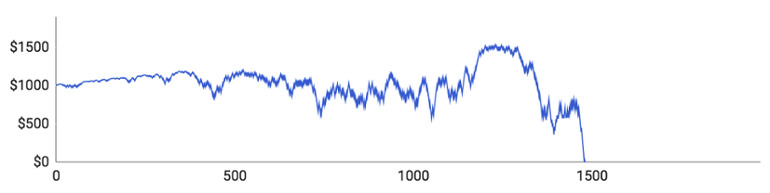
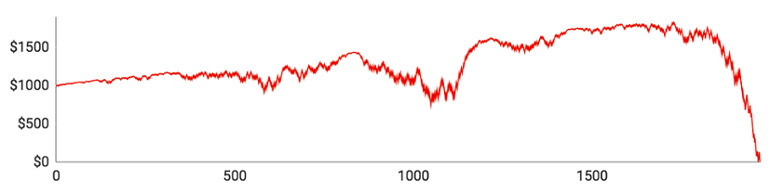
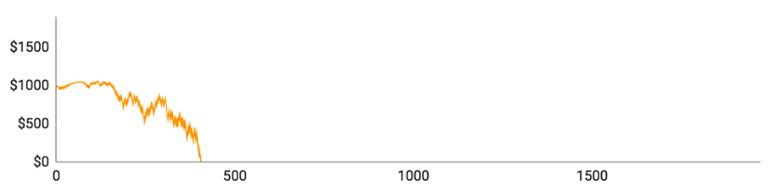
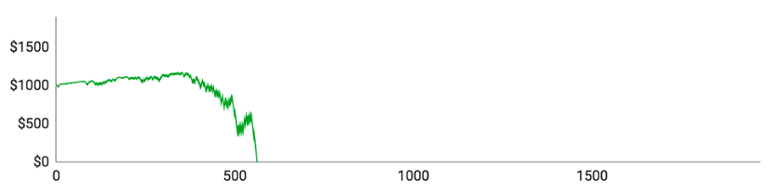
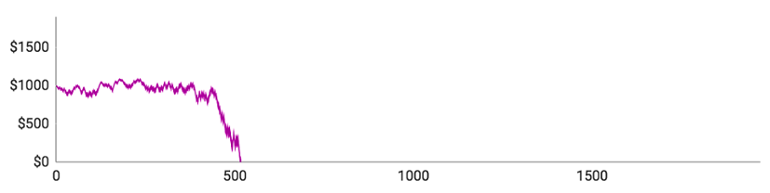
Lad os se på de individuelle spillere:
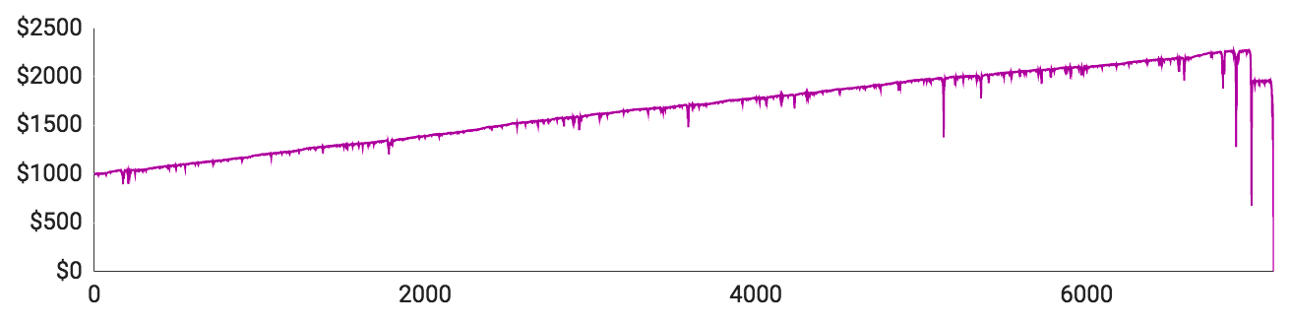
- Spiller #1 fik spillet 1480 runder, inden han løb tør for penge. Da det gik bedst, var han oppe på $1532. Hans indsatser blev større og større, og derfor blev hans op- og nedture også større og større. Hans største indsats i en enkelt runde var $58, og hans gennemsnitlige indsats omkring de $23,40.
- Spiller #2 fik de bedste resultater. Han nåede at spille 1971 runder i alt og var på et tidspunkt oppe på $1824. Kort efter røg han dog ind i en større nedgangsperiode, der sendte ham hele vejen ned til $0. Hans maksimale indsats var $62, men han spillede kun for $16,75 i gennemsnit, fordi han klarede sig bedre end gennemsnittet og derfor generelt kunne holde sine indsatser forholdsvis lave.
- Spiller #3 nåede kun at spille 406 runder og klarede sig ikke særlig godt. Han vandt kun 184 ud af sine 406 runder (45,3 %), hvilket er signifikant lavere end den forventede procentsats på 48,65 %. Hans toppunkt var $1056.
- Spiller #4 havde heller ikke heldet med sig. Han spillede 563 runder i alt og nåede op på $1172, da det gik bedst. Hans gennemsnitlige indsats var $14,70 og hans maksimale indsats var $50.
- Spiller #5’s forløb lignede på mange områder spiller #3’s. Han spillede kun 517 runder og nåede aldrig over $1086 på sin konto. Ud af de 517 runder vandt han kun 236 (45,7 %).
Som du kan se, havde vi særligt fokus på størrelsen af spillernes indsatser og procentdelen af gevinster og tab i forbindelse med D’Alembert-strategien. Det skyldes selvfølgelig, at strategien ifølge teorien bag skulle give overskud, hvis en spiller vinder lige så mange runder, som han taber. Det er bare svært på rouletten.
De 5 spillere spillede 4937 runder tilsammen, men de vandt kun 2366. De resterende 2571 blev tabt. Det betyder, at deres samlede vinderprocent var nede på 47,9 %. Da der var flere tab end gevinster, blev deres indsatser generelt højere og højere, og med højere indsatser kommer større opture og nedture.
Labouchere-strategien på roulette
Labouchere-strategien er den mest komplicerede af strategierne her i artiklen. Når du spiller efter den, er du nødt til at holde styr på dine indsatser og lægge tal sammen undervejs, hvilket kan kræve en del øvelse.
Labouchere-strategien fungerer på følgende måde:
- Du lægger ud med at konstruere en såkaldt "indsatslinje", der fastlægger din første indsats og til en vis grad også dine indsatser i de efterfølgende spilrunder. Du vælger helt selv, hvordan din linje skal se ud. Den kan være simpel som 1-1-1-1-1-1 eller 1-2-3-4-5-6 eller mere kompleks som 1-2-4-4-3-7.
- Du finder din indsats ved at tage et tal fra hver ende af linjen og lægge dem sammen. Summen af de to tal er din indsats i det pågældende spin.
- Hvis du taber, skriver du din netop tabte indsats ned for enden af linjen. Derefter går du tilbage til punkt #2 og fortsætter.
- Hvis du vinder, streger du de to tal ud på linjen. Derefter går du tilbage til punkt #2 og fortsætter.
- Hvis du løber tør for tal på din indsatslinje, begynder du enten forfra på din eksisterende linje eller konstruerer en ny.
Det er en smule kompliceret, så vi tager et eksempel for at illustrere pointen. Se tabellen nedenfor.
| Runde # | Aktuel indsatslinje | Indsats | Resultat af runden |
|---|---|---|---|
| 1 | 1-2-3-4-5-6 | 1 + 6 = 7 | TAB |
| 2 | 1-2-3-4-5-6-7 | 1 + 7 = 8 | GEVINST |
| 3 | 2-3-4-5-6 | 2 + 6 = 8 | TAB |
| 4 | 2-3-4-5-6-8 | 2 + 8 = 10 | TAB |
| 5 | 2-3-4-5-6-8-10 | 2 + 10 = 12 | GEVINST |
| 6 | 3-4-5-6-8 | 3 + 8 = 11 | GEVINST |
| 7 | 4-5-6 | 4 + 6 = 10 | ... |
Når du spiller efter Labouchere-strategien, er dit "mål" at slippe af med alle tallene på indsatslinjen. Hvis det lykkes, vil du have opnået et overskud, der svarer til summen af de tal, du havde på indsatslinjen til at begynde med, uanset hvor mange gange du vandt og tabte undervejs.
Matematikken fungerer ganske fornuftigt i strategien, men du skal som altid huske på, at statistikken giver casinoet en fordel. Selv med Labouchere-strategien er det altså ikke muligt at opnå overskud på rouletten i det lange løb.
Fordele og ulemper ved Labouchere-strategien
Labouchere-strategien befinder sig et sted mellem Fibonacci og D’Alembert, når det gælder risici. Matematikken bag er gennemtænkt, og du får overskud, hvis du vinder lige så mange runder, som du taber. Som du allerede ved, er det bare umuligt i længden.
Hvis du løber ind i en serie tab, vil tallene på din linje desuden vokse sig større og større. Din linje vil blive længere og længere, og du er nødt at satse flere og flere penge. Og som om det ikke var slemt nok, vil dine indsatser stadig være ret store i et stykke tid, efter du begynder at vinde. Det kræver en ret lang vinderstime at få dem ned igen.
Simulationer af Labouchere-strategien
Simulationerne af Labouchere-strategien er forholdsvis komplekse, fordi de afhænger af den indsatslinje, spillerne starter ud med. I vores simulationer har vi valgt følgende indsatslinje: 1-2-3-4-5-6.
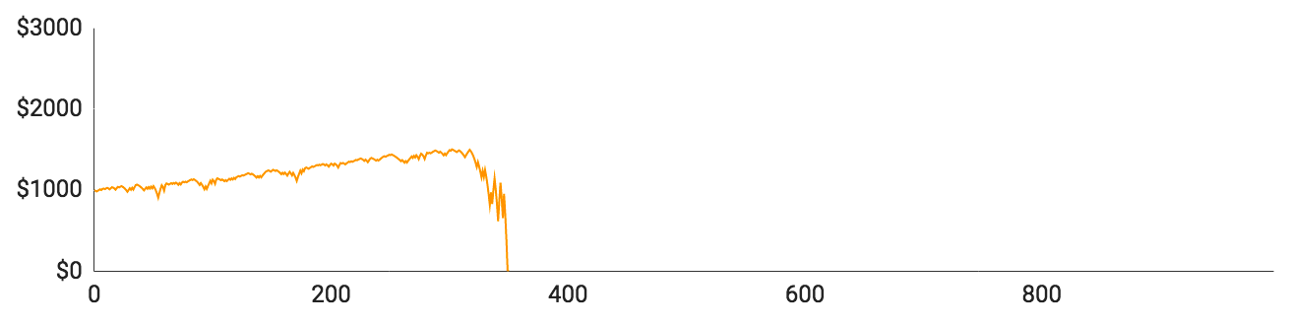
Her er graferne:
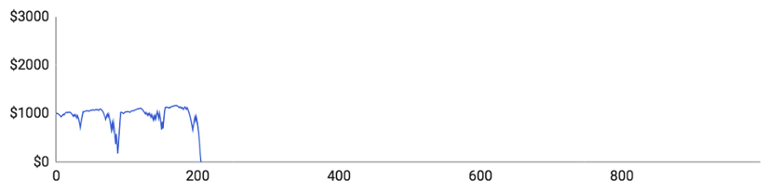
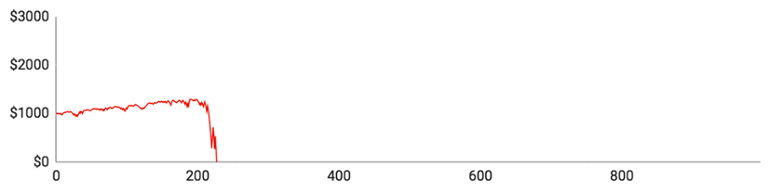
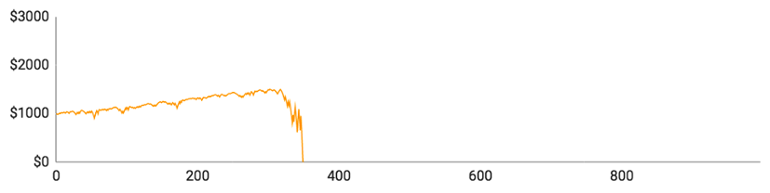
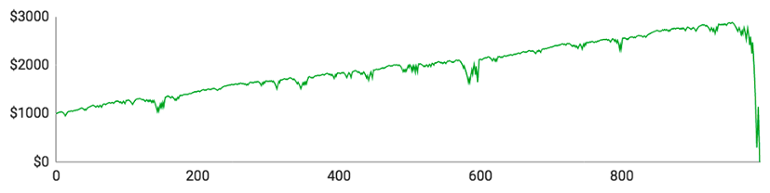
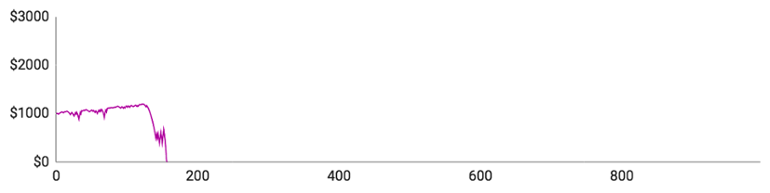
De individuelle spillere klarede sig som følger:
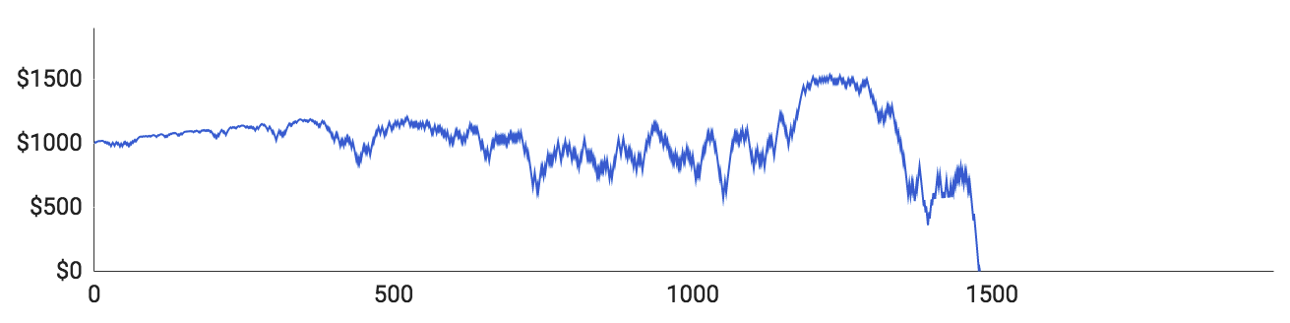
- Spiller #1 nåede op på 205 runder og havde $1170 på kontoen, da han var på sit højeste. Hans maksimale indsats var $240, og hans gennemsnitlige indsats var $44,65. Han klarede sig igennem en enkelt større nedtur, men blev kort efter ramt af en ny, så han løb tør for penge.
- Spiller #2 spillede 227 runder i alt og toppede med $1296 på lommen. Hans største indsats i en enkelt runde var $272, men han spillede i gennemsnit for $28,48 pr. runde.
- Spiller #3 nåede op på 350 runder og havde $1504 på kontoen, da det gik bedst. Hans maksimumindsats var $377, og hans gennemsnitlige indsats lige under $27. Han byggede stille og roligt sin saldo op, inden en enkelt stor taberstime frarøvede ham alt, hvad han ejede og havde.
- Spiller #4 havde et noget anderledes forløb. Han nåede at spille 996 runder på rouletten, hvilket var signifikant flere end alle hans kolleger. Han var på et tidspunkt helt oppe på $2881, fordi han vandt 52,1 % af sine spillede runder og derfor alt andet lige var temmelig heldig. På trods af sit held endte han dog alligevel med et stort rundt $0 på kontoen efter en langvarig serie af tab.
- Spiller #5 nåede op på 157 runder og havde $1201, da han toppede. Hans maksimale indsats var $205, og han spillede i gennemsnit for $31,57 pr. runde.
Resultaterne af vores simulation er ganske interessante, især for spiller #4, der klarede sig overraskende godt. De enkelte simulationer illustrerer fint ulemperne ved Labouchere-strategien – de stigende indsatser og de deraf følgende større op- og nedture.
Strategien (med en indsatslinje på 1-2-3-4-5-6) virker umiddelbart som den mest risikable af de fire strategier i vores artikel. Spillernes saldo steg i en fart, men til gengæld tabte de i gennemsnit også det hele hurtigst af alle, da det først gik galt. Det kunne selvfølgelig have set anderledes ud med en anden indsatslinje i simulationen.
Bedre strategier til roulette
Selvom strategierne i artiklen her umiddelbart ser ud til at virke, har ovenstående forhåbentlig vist, at det kun er et spørgsmål om tid, før du taber alle dine penge, hvis du spiller efter dem. Derfor kan vi naturligvis ikke anbefale dem.
Hvis du vil maksimere dine chancer for at få overskud på dit casinobesøg eller i det mindste sikre dig, at du får så meget underholdning for pengene som muligt, findes der langt bedre strategier. De kan selvfølgelig heller ikke give dig overskud på den lange bane, men de har en række andre kvaliteter. Hvis du er interesseret, er du velkommen til at læse vores artikel om roulettestrategier, der virker.